Transformations du plan
Homothéties
Les homothéties sont d'autres transformations du plan classiques, mais qui ne sont (généralement) pas des isométries.
Définissons d'abord l'homothétie de façon rigoureuse. L'image d'un point $P$ par l'homothétie de centre $O$ et de rapport $k$ est l'unique point $P'$ tel que $\vec{OP'} = k \cdot \vec{OP}$. Pour ceux ne connaissant pas les vecteurs, cela revient à dire la chose suivante :
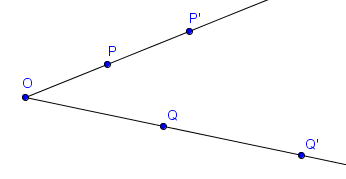
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $2$.
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $-2$.
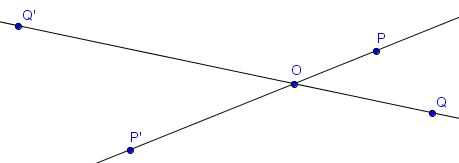
On remarque qu'appliquer une homothétie de centre $O$ et de rapport $k$ avec $k < 0$ revient exactement à effectuer une homothétie de rapport $|k|$ puis une symétrie centrale.
Définition
Étant donné un point $O$ du plan et un réel non-nul $k$, on définit l'homothétie de centre $O$ et de rapport $k$. Intuitivement, lorsque $k > 1$ cela consiste à zoomer la figure sur le point $O$ (et plus $k$ est grand, plus on zoome). Si $0 < k < 1$ alors il s'agit plutôt d'un dézoom de la figure, toujours centré en le point $O$. Le cas où $k < 0$ est un peu plus particulier : nous en discuterons plus bas.Définissons d'abord l'homothétie de façon rigoureuse. L'image d'un point $P$ par l'homothétie de centre $O$ et de rapport $k$ est l'unique point $P'$ tel que $\vec{OP'} = k \cdot \vec{OP}$. Pour ceux ne connaissant pas les vecteurs, cela revient à dire la chose suivante :
- Si $k > 0$, alors $P'$ est le point de la droite $OP$ du même côté de $O$ que $P$ et tel que $|OP'| = k \cdot |OP|$.
- Si $k < 0$, alors $P'$ est le point de la droite $OP$ du côté opposé de $O$ que $P$ et tel que $|OP'| = |k| \cdot |OP|$.
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $2$.

Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $-2$.

On remarque qu'appliquer une homothétie de centre $O$ et de rapport $k$ avec $k < 0$ revient exactement à effectuer une homothétie de rapport $|k|$ puis une symétrie centrale.
Propriétés
Mis à part lorsque $k = \pm 1$, on voit qu'une homothétie de rapport $k$ n'est pas une isométrie. Les homothéties ont toutefois des propriétés similaires aux isométries.Propriété des homothéties
Une homothétie de rapport $k$ :
- multiplie les longueurs par $|k|$ : $|P'Q'| = |k| \cdot |PQ|$;
- conserve l'amplitude des angles;
- conserve l'alignement des points;
- conserve le parallélisme des droites;
- conserve la perpendicularité des droites;
- conserve le milieu d'un segment;
- multiplie les périmètres des figures par $|k|$ et les aires des figures par $k^2$;
- envoie toute droite sur une droite parallèle.
- ...