Transformations du plan
Cercle d'Euler
Le cercle d'Euler d'un triangle, aussi appelé cercle des neufs points est le cercle dont l'existence est assurée par la proposition suivante. Nous conseillons vivement au lecteur d'essayer de comprendre sa démonstration, qui fait à nouveau intervenir des homothéties.
À noter que l'on peut retenir les points 2 et 3 en retenant simplement que le cercle d'Euler est l'image du cercle circonscrit par l'homothétie de centre $H$ et de rapport $\frac{1}{2}$. Comme les milieux des côtés et les pieds des hauteurs sont sur le cercle d'Euler, ces résultats en découlent.
Existence du cercle d'Euler
Théorème (cercle d'Euler)
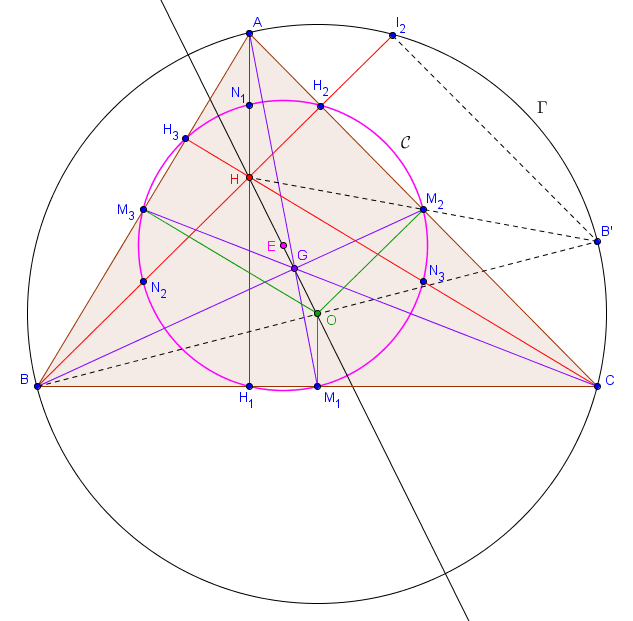
Soit $ABC$ un triangle, $M_1, M_2, M_3$ les milieux des côtés $[BC]$, $[CA]$ et $[AB]$, $H$ l'orthocentre de $ABC$, et $H_1, H_2, H_3$ les pieds des hauteurs relatives à $A$, $B$ et $C$. Il existe un unique cercle passant par $M_1, M_2, M_3, H_1, H_2, H_3$ ainsi que les milieux de $[HA]$, $[HB]$ et $[HC]$. Ce cercle est appelé le cercle d'Euler de $ABC$, et son centre se situe sur la droite d'Euler de $ABC$.
Démonstration
Considérons tout d'abord l'homothétie $h_G$ de centre $G$ et de rapport $-\frac{1}{2}$. Nous avons déjà vu dans le point théorique précédent que $h_G$ envoie $A$, $B$ et $C$ sur $M_1$, $M_2$ et $M_3$ respectivement, ainsi que $H$ sur $O$, le centre du cercle circonscrit à $ABC$. En particulier, le cercle circonscrit $\Gamma$ à $ABC$ a pour image le cercle circonscrit à $M_1M_2M_3$. Notons ce dernier cercle $\mathcal{C}$. Celui-ci passe par $M_1$, $M_2$ et $M_3$ et on sait déjà que son centre $E$ est l'image de $O$ par l'homothétie $h_G$. Cela signifie que $E$ se situe sur la droite d'Euler, et on sait même que $|EG| = \frac{1}{2} \cdot |GO|$ (avec $G \in [OE]$). $(1)$
Nous devons à présent montrer que le cercle $\mathcal{C}$ contient également les six autres points mentionnés dans l'énoncé. Avant cela, remarquons la chose suivante. Notons $B'$ le symétrique de $B$ par rapport à $O$. Comme $O$ est le centre de $\Gamma$, il est clair que $B' \in \Gamma$. De plus, l'image du segment $[BH]$ par $h_G$ est le segment $[M_2O]$. Cela signifie que, dans le triangle $B'BH$, le segment $[M_2O]$ est le segment reliant les milieux de deux côtés. Il en découle que $M_2$ est le milieu de $[B'H]$. Nous venons donc de montrer que le symétrique de $H$ par rapport à $M_2$, qui n'est autre que $B'$, appartient à $\Gamma$. De manière similaire, on trouve en fait que les symétriques de $H$ par rapport aux trois milieux $M_1, M_2, M_3$ sont tous sur $\Gamma$. $(2)$
Considérons à présent l'homothétie $h_H$ de centre $H$ et de rapport $\frac{1}{2}$. Nous venons en fait juste de prouver que l'image de $B'$ par $h_H$ est $M_2$. De la même manière, $M_1$ et $M_3$ sont les images par $h_H$ de deux points du cercle $\Gamma$. Il en découle que $\mathcal{C}$ est l'image de $\Gamma$ par $h_H$. (À noter qu'on a déjà vu que $\mathcal{C}$ était l'image de $\Gamma$ par $h_G$ qui est une toute autre homothétie ! Tout cela est plutôt magique.) Comme les images de $A$, $B$ et $C$ (qui se situent sur $\Gamma$) par $h_H$ sont les milieux respectifs de $[AH]$, $[BH]$ et $[CH]$, on en déduit que ces milieux se trouvent sur $\mathcal{C}$.
Enfin, notons $I_2$ la deuxième intersection de $BH$ avec $\Gamma$. Comme $[BB']$ est un diamètre de $\Gamma$, le triangle $BI_2B'$ est rectangle en $I_2$. Il s'ensuit que $B'I_2$ est parallèle à $AC$. Comme $M_2$ est le milieu de $[B'H]$, cela signifie que $[M_2H_2]$ est le segment joignant les milieux de deux côtés du triangle $HB'I_2$ et donc en particulier que $H_2$ est le milieu de $[HI_2]$. Les symétriques de l'orthocentre par rapport aux côtés se trouvent donc tous sur $\Gamma$, ce qui est à nouveau un résultat remarquable $(3)$. L'image de $I_2$ par $h_H$ est donc exactement $H_2$, et cela implique que $H_2 \in \mathcal{C}$. De la même manière, on trouve que $H_1$ et $H_3$ se situent sur $\mathcal{C}$.
Nous devons à présent montrer que le cercle $\mathcal{C}$ contient également les six autres points mentionnés dans l'énoncé. Avant cela, remarquons la chose suivante. Notons $B'$ le symétrique de $B$ par rapport à $O$. Comme $O$ est le centre de $\Gamma$, il est clair que $B' \in \Gamma$. De plus, l'image du segment $[BH]$ par $h_G$ est le segment $[M_2O]$. Cela signifie que, dans le triangle $B'BH$, le segment $[M_2O]$ est le segment reliant les milieux de deux côtés. Il en découle que $M_2$ est le milieu de $[B'H]$. Nous venons donc de montrer que le symétrique de $H$ par rapport à $M_2$, qui n'est autre que $B'$, appartient à $\Gamma$. De manière similaire, on trouve en fait que les symétriques de $H$ par rapport aux trois milieux $M_1, M_2, M_3$ sont tous sur $\Gamma$. $(2)$
Considérons à présent l'homothétie $h_H$ de centre $H$ et de rapport $\frac{1}{2}$. Nous venons en fait juste de prouver que l'image de $B'$ par $h_H$ est $M_2$. De la même manière, $M_1$ et $M_3$ sont les images par $h_H$ de deux points du cercle $\Gamma$. Il en découle que $\mathcal{C}$ est l'image de $\Gamma$ par $h_H$. (À noter qu'on a déjà vu que $\mathcal{C}$ était l'image de $\Gamma$ par $h_G$ qui est une toute autre homothétie ! Tout cela est plutôt magique.) Comme les images de $A$, $B$ et $C$ (qui se situent sur $\Gamma$) par $h_H$ sont les milieux respectifs de $[AH]$, $[BH]$ et $[CH]$, on en déduit que ces milieux se trouvent sur $\mathcal{C}$.
Enfin, notons $I_2$ la deuxième intersection de $BH$ avec $\Gamma$. Comme $[BB']$ est un diamètre de $\Gamma$, le triangle $BI_2B'$ est rectangle en $I_2$. Il s'ensuit que $B'I_2$ est parallèle à $AC$. Comme $M_2$ est le milieu de $[B'H]$, cela signifie que $[M_2H_2]$ est le segment joignant les milieux de deux côtés du triangle $HB'I_2$ et donc en particulier que $H_2$ est le milieu de $[HI_2]$. Les symétriques de l'orthocentre par rapport aux côtés se trouvent donc tous sur $\Gamma$, ce qui est à nouveau un résultat remarquable $(3)$. L'image de $I_2$ par $h_H$ est donc exactement $H_2$, et cela implique que $H_2 \in \mathcal{C}$. De la même manière, on trouve que $H_1$ et $H_3$ se situent sur $\mathcal{C}$.

Propriétés annexes
Au cours de la preuve précédente, certains résultats annexes sont apparus (dont les énoncés ne font pas toujours intervenir le cercle d'Euler, ce qui les rend donc peut-être d'autant plus intéressants). Nous les mettons à nouveau en évidence ici (voir $(1)$, $(2)$ et $(3)$ dans la preuve pour les démonstrations).Autres propriétés
- La droite d'Euler contient le centre du cercle d'Euler, et on a $|OG| = 2 \cdot |GE|$ (avec $G \in [EO]$).
- Les trois symétriques de l'orthocentre par rapport aux milieux des côtés se trouvent sur le cercle circonscrit.
- Les trois symétriques de l'orthocentre par rapport aux côtés se trouvent sur le cercle circonscrit.
À noter que l'on peut retenir les points 2 et 3 en retenant simplement que le cercle d'Euler est l'image du cercle circonscrit par l'homothétie de centre $H$ et de rapport $\frac{1}{2}$. Comme les milieux des côtés et les pieds des hauteurs sont sur le cercle d'Euler, ces résultats en découlent.
Théorème de Feuerbach
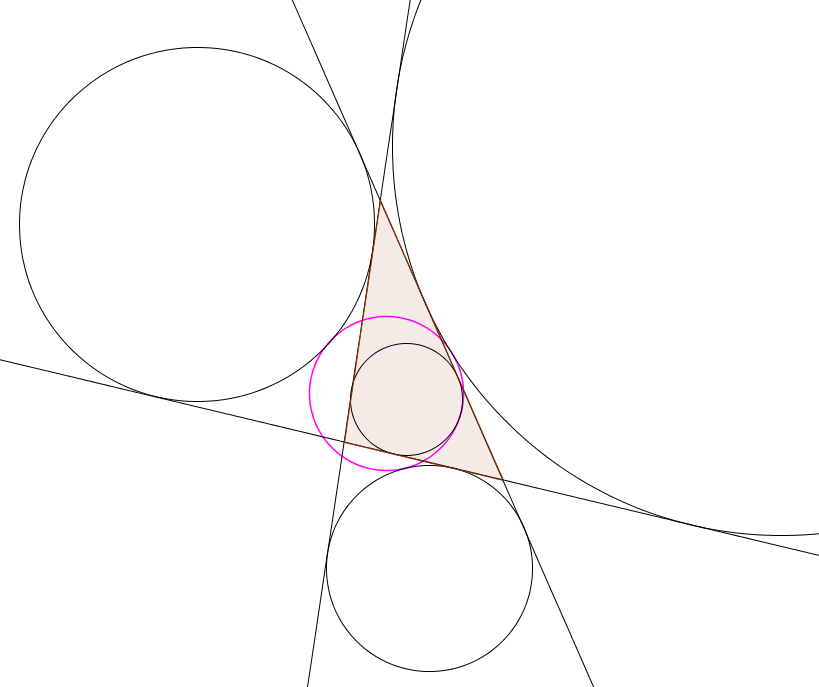
Le cercle d'Euler a également la propriété d'être tangent intérieurement au cercle inscrit et tangent extérieurement aux trois cercles exinscrits au triangle. Ce résultat est appelé théorème de Feuerbach, et les quatre points de tangence sont appelés les points de Feuerbach.