Inversion et polarisation
Inversion
Les inversions sont des transformations du plan très particulières, de par le fait qu'elles modifient complètement les objets présents sur la figure. Comme nous allons le voir, les inversions transforment certains cercles en droites, et c'est une des raisons pour lesquelles elles peuvent être très utiles. En effet, en présence d'une figure contenant beaucoup de cercles, il peut parfois se révéler utile d'appliquer une inversion pour transformer la plupart de ces cercles en droites, objets que l'on maîtrise généralement mieux. Aussi, comme pour les transformations du plan classiques, remarquer dans un problème que certains objets sont images de certains autres par une inversion particulière peut permettre de progresser dans sa résolution.
Étant donnés un point $O$ du plan et un réel $k > 0$, on définit l'inversion de centre $O$ et de rapport $k$ en disant que l'image d'un point $P$ différent de $O$ est l'unique point $P'$ appartenant à la demi-droite $[OP$ et tel que $|OP| \cdot |OP'| = k$. De manière générale, on peut en fait aussi définir l'inversion de centre $O$ et de rapport $k$ lorsque $k < 0$. Celle-ci revient à effectuer l'inversion de centre $O$ et de rapport $|k|$ puis la symétrie centrale de centre $O$.
En général, lorsque l'on désire effectuer une inversion, on ne donne pas réellement la valeur de $k$. On précise plutôt l'image d'un point particulier. Par exemple, si l'on est en présence de trois points $O$, $A$ et $A'$ alignés, on peut parler de l'inversion de centre $O$ envoyant $A$ sur $A'$. Cela revient exactement à dire que l'on considère l'inversion de centre $O$ et de rapport $k = |OA| \cdot |OA'|$ (ou $-|OA| \cdot |OA'|$ si $A$ et $A'$ ne sont pas du même côté de $O$).
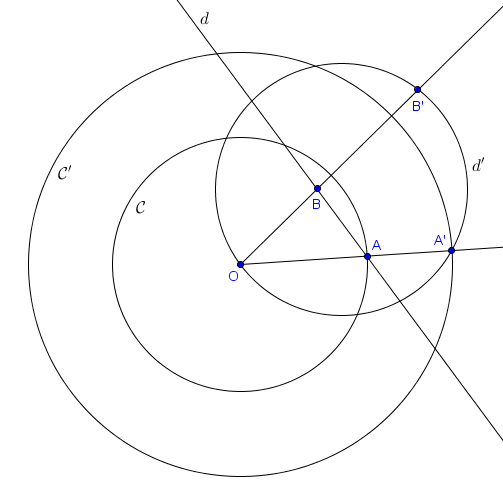
Il découle de la définition d'inversion que si un point $P$ a pour image $P'$ (par une certaine inversion), alors le point $P'$ a pour image $P$. Sur l'exemple ci-dessus, l'image de $A'$ par l'inversion est donc $A$, l'image de $\mathcal{C'}$ est $\mathcal{C}$, l'image de $B'$ est $B$, et l'image du cercle $d'$ est la droite $d$.
On a aussi la propriété suivante, dont la démonstration est une application directe de la définition d'inversion. La figure plus haut permet de mieux visualiser la propriété.
Définition
Intuitivement, une inversion de centre $O$ va être telle que les points éloignés de $O$ en deviendront proches, et vice versa.Étant donnés un point $O$ du plan et un réel $k > 0$, on définit l'inversion de centre $O$ et de rapport $k$ en disant que l'image d'un point $P$ différent de $O$ est l'unique point $P'$ appartenant à la demi-droite $[OP$ et tel que $|OP| \cdot |OP'| = k$. De manière générale, on peut en fait aussi définir l'inversion de centre $O$ et de rapport $k$ lorsque $k < 0$. Celle-ci revient à effectuer l'inversion de centre $O$ et de rapport $|k|$ puis la symétrie centrale de centre $O$.
En général, lorsque l'on désire effectuer une inversion, on ne donne pas réellement la valeur de $k$. On précise plutôt l'image d'un point particulier. Par exemple, si l'on est en présence de trois points $O$, $A$ et $A'$ alignés, on peut parler de l'inversion de centre $O$ envoyant $A$ sur $A'$. Cela revient exactement à dire que l'on considère l'inversion de centre $O$ et de rapport $k = |OA| \cdot |OA'|$ (ou $-|OA| \cdot |OA'|$ si $A$ et $A'$ ne sont pas du même côté de $O$).
Exemple
Pour bien comprendre la notion d'inversion, observons un exemple. Sur la figure suivante, nous considérons l'inversion de centre $O$ envoyant $A$ sur $A'$. Le cercle $\mathcal{C}$ de centre $O$ et passant par $A$ est alors logiquement envoyé sur le cercle $\mathcal{C'}$ de centre $O$ et passant par $A'$. L'image du point $B$ par l'inversion est notée $B'$. Puisque $B$ se situe à l'intérieur de $\mathcal{C}$, on a $|OB| < |OA|$. Il découle alors de la définition que $B'$ doit vérifier $|OB'| > |OA'|$. C'est pourquoi $B'$ se situe à l'extérieur de $\mathcal{C'}$. Le plus intéressant, sur cet exemple, est le cas de la droite $d = AB$. On sait que l'image de cette droite doit passer par $A'$ et par $B'$. D'autre part, les points de $d$ se situant très loin de $O$ doivent avoir pour image des points très proches de $O$. On dit souvent par abus de langage que "le point à l'infini est envoyé sur $O$" et réciproquement que "$O$ est envoyé sur le point à l'infini". Il est en fait possible de montrer rigoureusement que l'image de la droite $d$ est exactement le cercle $d'$ passant par $A'$, $B'$ et $O$.
Il découle de la définition d'inversion que si un point $P$ a pour image $P'$ (par une certaine inversion), alors le point $P'$ a pour image $P$. Sur l'exemple ci-dessus, l'image de $A'$ par l'inversion est donc $A$, l'image de $\mathcal{C'}$ est $\mathcal{C}$, l'image de $B'$ est $B$, et l'image du cercle $d'$ est la droite $d$.
Propriétés
Nous donnons à présent les propriétés essentielles des inversions. Nous avons déjà observé certaines de celles-ci sur notre exemple, et nous conseillons au lecteur de dessiner les nouvelles propriétés pour se familiariser avec elles.Propriétés (inversions)
Une inversion de centre $O$ et de rapport $k$ :
- envoie une droite passant par $O$ sur elle-même;
- envoie une droite ne passant pas par $O$ sur un cercle passant par $O$;
- envoie un cercle centré en $O$ sur un cercle centré en $O$ (en particulier, le cercle centré en $O$ et de rayon $\sqrt{|k|}$ est envoyé sur lui-même);
- envoie un cercle passant par $O$ sur une droite ne contenant pas $O$;
- envoie un cercle renfermant $O$ sur un cercle renfermant $O$;
- envoie un cercle ne renfermant pas $O$ sur un cercle ne renfermant pas $O$.
On a aussi la propriété suivante, dont la démonstration est une application directe de la définition d'inversion. La figure plus haut permet de mieux visualiser la propriété.
Propriété
Soient $O$, $A$ et $B$ trois points non-alignés du plan et $k$ un réel non-nul. Si $A'$ et $B'$ sont les images respectives de $A$ et $B$ par l'inversion de centre $O$ et de rapport $k$, alors les triangles $OA'B'$ et $OBA$ sont semblables.
Démonstration
On a par définition que $|OA| \cdot |OA'| = |OB| \cdot |OB'|$, donc $\dfrac{|OA|}{|OB|} = \dfrac{|OB'|}{|OA'|}$. Puisque de plus, $\widehat{AOB} = \widehat{A'OB'}$, les triangles $OA'B'$ et $OBA$ sont semblables.