Théorie > Géométrie > Inversion et polarisation
Polarisation
Étant donné un cercle de centre $O$ et de rayon $R$ dans le plan, on peut également considérer la polarisation par rapport à ce cercle. Ce qui distingue cette transformation de toutes celles qui ont déjà été étudiées sur ce site, c'est que l'image d'un point n'est plus un point mais une droite. Il ne s'agit donc pas réellement d'une transformation du plan qui peut être appliquée à toute une figure. On dira juste que certaines droites sont les polaires de certains points, et on essayera d'en déduire des informations utiles à partir des propriétés de la polarisation.
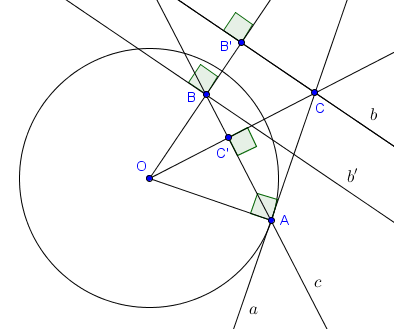
Sur la figure suivante, on considère la polarisation par rapport au cercle de centre $O$ passant par $A$. La polaire de $A$ est la droite $a$ tangente au cercle et passant par $A$. Les polaires respectives de $B$ et $B'$ sont les droites $b$ et $b'$ (car, sur cette figure, $B'$ est l'image de $B$ par l'inversion de centre $O$ et de rapport $|OA|^2$). Un fait important, qui fait appel aux propriétés des polarisations, est que la polaire du point $C$ (intersection de $a$ et $b$) est exactement la droite $c$ passant par $A$ et $B$.
Une autre propriété utile, mais moins évidente, est la suivante. Une façon de la prouver est d'utiliser le théorème de Pascal.
À noter que les points $A, B, C, D$ peuvent être dans un ordre quelconque sur le cercle. Cela signifie donc que la polaire de $Q$ est $PR$ et que la polaire de $R$ est $PQ$.
Avant cela, signalons le fait remarquable suivant : dans un triangle, la polaire du point de Lemoine par rapport au cercle circonscrit au triangle est exactement la droite de Lemoine du triangle. Les définitions du point et de la droite de Lemoine sont données dans les chapitres Triangles (suite) et Cercles d'Apollonius respectivement.
Définition
Fixons un cercle $\mathcal{C}$ de centre $O$ et de rayon $R$. Étant donné un point $P$ différent de $O$, on définit la polaire de $P$ par rapport à $\mathcal{C}$ comme suit. Soit $P'$ l'image de $P$ par l'inversion de centre $O$ et de rapport $R^2$, c'est-à-dire l'unique point de $[OP)$ tel que $|OP| \cdot |OP'| = R^2$. Alors la polaire de $P$ est définie comme étant la droite perpendiculaire à $OP$ et passant par $P'$. Si $d$ est la polaire de $P$ par rapport à $\mathcal{C}$, alors on dit aussi que $P$ est le pôle de $d$ (par rapport à $\mathcal{C}$).Sur la figure suivante, on considère la polarisation par rapport au cercle de centre $O$ passant par $A$. La polaire de $A$ est la droite $a$ tangente au cercle et passant par $A$. Les polaires respectives de $B$ et $B'$ sont les droites $b$ et $b'$ (car, sur cette figure, $B'$ est l'image de $B$ par l'inversion de centre $O$ et de rapport $|OA|^2$). Un fait important, qui fait appel aux propriétés des polarisations, est que la polaire du point $C$ (intersection de $a$ et $b$) est exactement la droite $c$ passant par $A$ et $B$.

Propriétés
Tout comme les inversions, les polarisations ont beaucoup de propriétés assez naturelles. Celles-ci ne sont pas compliquées à démontrer (et il peut être bon, comme exercice, d'essayer d'en donner une démonstration). Pour autant, elles n'en sont pas moins essentielles.Propriétés (polarisations)
Considérons une polarisation par rapport à un cercle $\mathcal{C}$ de centre $O$ et de rayon $R$.
- La polaire d'un point $P$ appartenant à $\mathcal{C}$ est la tangente à $\mathcal{C}$ en $P$.
- La polaire d'un point $P$ intérieur à $\mathcal{C}$ est une droite extérieure à $\mathcal{C}$.
- La polaire d'un point $P$ extérieur à $\mathcal{C}$ peut être construite comme suit : soient $S$ et $T$ les points de tangence des deux tangentes à $\mathcal{C}$ issues de $P$. Alors la polaire de $P$ est la droite $ST$.
- Si un point $P$ se trouve sur la polaire d'un point $Q$, alors $Q$ se situe sur la polaire de $P$.
- Si deux points $A$ et $B$ ont pour polaires deux droites s'intersectant en un point $C$, alors la polaire de $C$ est la droite $AB$.
- Les polaires de trois points alignés sont concourantes. (NB : si les trois points sont également alignés avec $O$, alors les droites sont concourantes "à l'infini", ce qui signifie qu'elles sont parallèles.)
Une autre propriété utile, mais moins évidente, est la suivante. Une façon de la prouver est d'utiliser le théorème de Pascal.
Propriété
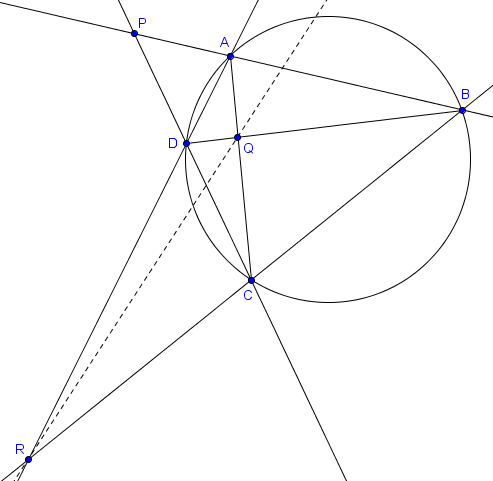
- Soient $A, B, C, D$ quatre points sur un cercle $\mathcal{C}$. On note $P$ l'intersection de $AB$ et $CD$, $Q$ l'intersection de $AC$ et $BD$, et $R$ l'intersection de $AD$ et $BC$ (en supposant qu'elles existent). Alors la polaire de $P$ par rapport à $\mathcal{C}$ est la droite $QR$.
À noter que les points $A, B, C, D$ peuvent être dans un ordre quelconque sur le cercle. Cela signifie donc que la polaire de $Q$ est $PR$ et que la polaire de $R$ est $PQ$.

Utilisation
Comme d'habitude, remarquer dans un problème qu'une certaine droite est la polaire d'un certain point (par rapport à un certain cercle) peut donner l'idée d'étudier cette polarisation plus en profondeur et de regarder quels sont les polaires des points de la figure. Dans le point théorique suivant, nous donnons deux exemples d'applications d'une polarisation qui permettent de résoudre un problème de géométrie.Avant cela, signalons le fait remarquable suivant : dans un triangle, la polaire du point de Lemoine par rapport au cercle circonscrit au triangle est exactement la droite de Lemoine du triangle. Les définitions du point et de la droite de Lemoine sont données dans les chapitres Triangles (suite) et Cercles d'Apollonius respectivement.