Théorie > Géométrie > Angles
Chasse aux angles
La première étape dans la résolution de tout problème de géométrie est la chasse aux angles. Elle consiste à trouver, sur la figure relative à l'énoncé du problème, tous les angles ayant la même amplitude. Cette chasse aux angles permet souvent d'identifier des droites parallèles ou perpendiculaires, des triangles semblables, ou encore des quadrilatères cycliques (nous verrons ce dont il s'agit par la suite).
Pour trouver ces angles ayant la même amplitude, on peut donner une valeur (par exemple $\alpha$ ou $\beta$) à un ou plusieurs angles semblant intéressants et en déduire les valeurs des autres angles de la figure. On peut pour cela utiliser les égalités dont nous avons parlé précédemment : les angles opposés par le sommets, les angles correspondants, les angles alternes-internes, les angles inscrits, tangentiels, au centre... On peut également utiliser que la somme des amplitudes des angles d'un même triangle vaut toujours $180^\circ$, que les triangles isocèles possèdent deux angles égaux, etc...
Le problème suivant est un problème d'Olympiades Internationales (2000, problème 1). Nous allons voir comment la chasse aux angles permet à elle seule de trouver un grand nombre d'informations. Il s'agit en fait là d'une partie essentielle dans la résolution de ce problème.
Pour trouver ces angles ayant la même amplitude, on peut donner une valeur (par exemple $\alpha$ ou $\beta$) à un ou plusieurs angles semblant intéressants et en déduire les valeurs des autres angles de la figure. On peut pour cela utiliser les égalités dont nous avons parlé précédemment : les angles opposés par le sommets, les angles correspondants, les angles alternes-internes, les angles inscrits, tangentiels, au centre... On peut également utiliser que la somme des amplitudes des angles d'un même triangle vaut toujours $180^\circ$, que les triangles isocèles possèdent deux angles égaux, etc...
Le problème suivant est un problème d'Olympiades Internationales (2000, problème 1). Nous allons voir comment la chasse aux angles permet à elle seule de trouver un grand nombre d'informations. Il s'agit en fait là d'une partie essentielle dans la résolution de ce problème.
Problème (IMO 2000, P1)
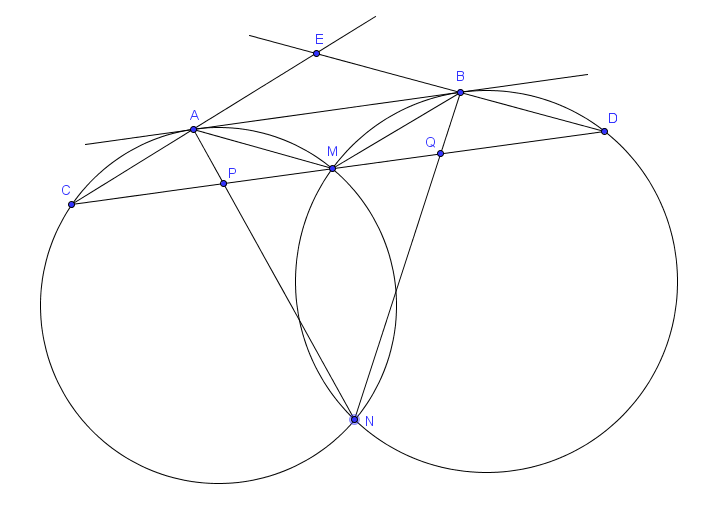
Deux cercles $G_1$ et $G_2$ s'intersectent en deux points $M$ et $N$. Soit $AB$ la droite tangente à ces cercles en $A$ et $B$, respectivement, de sorte que $M$ soit plus proche de $AB$ que $N$. Soit $CD$ la droite parallèle à $AB$ et passant par $M$, avec $C$ sur $G_1$ et $D$ sur $G_2$. Les droites $AC$ et $BD$ se rencontrent en $E$, les droites $AN$ et $CD$ se rencontrent en $P$ et les droites $BN$ et $CD$ se rencontrent en $Q$. Prouver que $|EP| = |EQ|$.

Début de démonstration
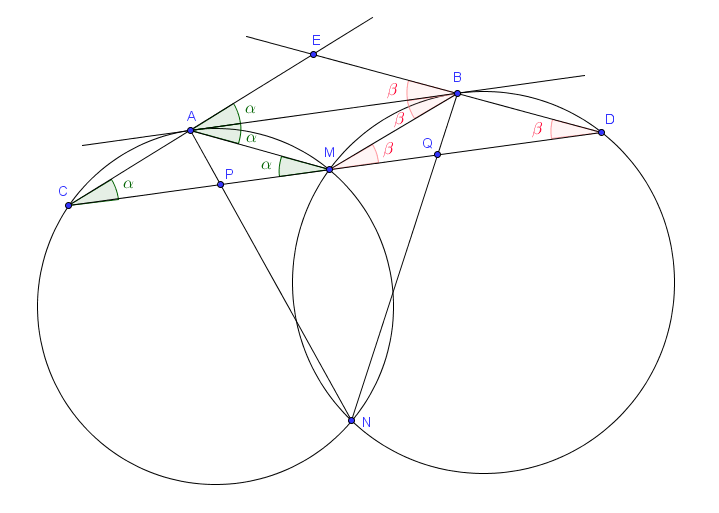
Pour notre chasse aux angles, on pose $\alpha = \widehat{EAB}$. On a alors :
De la même façon, on pose $\beta = \widehat{EBA}$ et on trouve pareillement $\widehat{EDM} = \widehat{ABM} = \widehat{BMD} = \beta$. Le triangle $BMD$ est donc à son tour isocèle.
Notre chasse aux angles nous a donc permis de prouver cette perpendicularité. Et celle-ci est très intéressante pour ce que nous avons à montrer ! En effet, on veut prouver que $|EP| = |EQ|$, mais maintenant que l'on sait que $EM \perp PQ$, on est simplement ramené à prouver que $|MP| = |MQ|$.
Pour montrer cette dernière égalité, il faut connaître quelques outils supplémentaires en géométrie, mais nous voyons qu'une simple chasse aux angles peut permettre de considérablement progresser dans la résolution d'un problème. Il est d'ailleurs très rare de rencontrer un problème où aucune chasse aux angles n'est nécessaire.
- $\widehat{ECM} = \widehat{EAB} = \alpha$ par angles correspondants,
- $\widehat{BAM} = \widehat{ACM} = \alpha$ car il s'agit d'angles inscrit et tangentiel interceptant le même arc,
- $\widehat{AMC} = \widehat{BAM} = \alpha$ par angles alternes-internes,
De la même façon, on pose $\beta = \widehat{EBA}$ et on trouve pareillement $\widehat{EDM} = \widehat{ABM} = \widehat{BMD} = \beta$. Le triangle $BMD$ est donc à son tour isocèle.

Notre chasse aux angles nous a donc permis de prouver cette perpendicularité. Et celle-ci est très intéressante pour ce que nous avons à montrer ! En effet, on veut prouver que $|EP| = |EQ|$, mais maintenant que l'on sait que $EM \perp PQ$, on est simplement ramené à prouver que $|MP| = |MQ|$.
Pour montrer cette dernière égalité, il faut connaître quelques outils supplémentaires en géométrie, mais nous voyons qu'une simple chasse aux angles peut permettre de considérablement progresser dans la résolution d'un problème. Il est d'ailleurs très rare de rencontrer un problème où aucune chasse aux angles n'est nécessaire.