Théorie > Géométrie > Cercles d'Apollonius
Triangle podaire
Il existe un lien entre les cercles d'Apollonius et la notion de triangle podaire. Rappelons que si $ABC$ est un triangle et $P$ un point, le triangle podaire $A'B'C'$ est défini en considérant les projections de $P$ sur les trois côtés du triangle, comme dans la figure suivante.
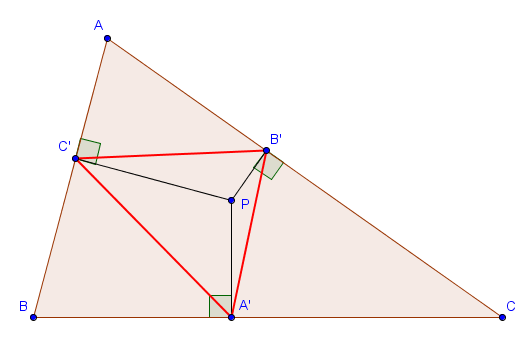
Comme nous l'avons déjà constaté, les longueurs des côtés de $A'B'C'$ sont données par les formules suivantes
$$|B'C'| = |PA| \cdot \sin \hat A, \quad |C'A'| = |PB| \cdot \sin \hat B, \quad |A'B'| = |PC| \cdot \sin \hat C.$$ On peut notamment en déduire que $|A'B'| = |A'C'|$ si et seulement si
$$1 = \frac{|A'B'|}{|A'C'|} = \frac{|PC| \cdot \sin \hat C}{|PB| \cdot \sin \hat B} = \frac{|PC|\cdot |AB|}{|PB| \cdot |AC|},$$ c'est-à-dire si et seulement si
$$\frac{|PC|}{|PB|} = \frac{|AC|}{|AB|}.$$ Nous venons donc de prouver le résultat suivant :
Il n'y aura bien sûr jamais un énoncé de géométrie contenant le terme Cercle d'Apollonius, mais l'intérêt de ceux-ci est que leur connaissance peut permettre de trouver plus rapidement une solution à un problème. Par exemple, si un triangle podaire est construit d'une façon ou d'une autre dans un énoncé (en projetant un même point $P$ sur plusieurs droites) et si celui-ci se révèle être isocèle, alors on peut directement en conclure que $P$ est sur le cercle d'Apollonius correspondant. On a donc un cercle passant par $P$ et plusieurs points remarquables, ce qui peut permettre de continuer avec une chasse aux angles, des puissances de points ou d'autres outils habituels...

Comme nous l'avons déjà constaté, les longueurs des côtés de $A'B'C'$ sont données par les formules suivantes
$$|B'C'| = |PA| \cdot \sin \hat A, \quad |C'A'| = |PB| \cdot \sin \hat B, \quad |A'B'| = |PC| \cdot \sin \hat C.$$ On peut notamment en déduire que $|A'B'| = |A'C'|$ si et seulement si
$$1 = \frac{|A'B'|}{|A'C'|} = \frac{|PC| \cdot \sin \hat C}{|PB| \cdot \sin \hat B} = \frac{|PC|\cdot |AB|}{|PB| \cdot |AC|},$$ c'est-à-dire si et seulement si
$$\frac{|PC|}{|PB|} = \frac{|AC|}{|AB|}.$$ Nous venons donc de prouver le résultat suivant :
Résultat
Soit $ABC$ un triangle et $P$ un point. Le triangle podaire $A'B'C'$ issu de $P$ est isocèle en $A'$ si et seulement si $P$ se situe sur le $A$-cercle d'Apollonius de $ABC$. En particulier, le triangle $A'B'C'$ est équilatéral si et seulement si $P$ est l'un des deux points d'intersection des trois cercles d'Apollonius.
Il n'y aura bien sûr jamais un énoncé de géométrie contenant le terme Cercle d'Apollonius, mais l'intérêt de ceux-ci est que leur connaissance peut permettre de trouver plus rapidement une solution à un problème. Par exemple, si un triangle podaire est construit d'une façon ou d'une autre dans un énoncé (en projetant un même point $P$ sur plusieurs droites) et si celui-ci se révèle être isocèle, alors on peut directement en conclure que $P$ est sur le cercle d'Apollonius correspondant. On a donc un cercle passant par $P$ et plusieurs points remarquables, ce qui peut permettre de continuer avec une chasse aux angles, des puissances de points ou d'autres outils habituels...