Théorie > Géométrie > Rapports anharmoniques

Général
Résumé Chapitre entier
Points théoriques
Définitions Dans la nature Théorèmes de Pascal et Pappus Théorème de Desargues Plan projectif réel
Exercices
Exercice 1 Exercice 2 Exercice 3 Exercice 4 Exercice 5

Théorèmes de Pascal et Pappus

Dans cette section nous expliquons comment les rapports anharmoniques peuvent être utilisés pour démontrer les théorèmes de Pascal et de Pappus. Cela nécessite d'abord de mettre en évidence quelques propriétés intéressantes des rapports anharmoniques.

Droites concourantes

Nous avons vu que deux droites sécantes à quatre mêmes droites concourantes donnent le même rapport anharmonique entre les points d'intersection. Ci-dessous nous formulons une sorte de réciproque qui peut se révéler bien pratique : si nous observons un même rapport anharmonique dans une situation bien précise, alors on peut en déduire que les droites reliant les points concernés sont concourantes.

Proposition
Soit $\ell$ et $\ell'$ deux droites sécantes s'intersectant en $A$. Considérons $B, C, D$ trois points sur $\ell$ et $B',C',D'$ trois points sur $\ell'$. Si $(A,B;C,D) = (A,B';C',D')$, alors les droites $BB'$, $CC'$ et $DD'$ sont concourantes.

Démonstration
Notons $O$ le point d'intersection de $CC'$ et $DD'$, et désignons par $B''$ l'intersection de $OB$ avec $\ell'$. On sait que $(A,B;C,D) = (A,B'';C',D')$, et par hypothèse que $(A,B;C,D) = (A,B';C',D')$. Donc $(A,B';C',D') = (A,B'';C',D')$, et par unicité du conjugué harmonique on en déduit que $B' = B''$. Donc $O \in BB'$, ce qui montre que les trois droites $BB'$, $CC'$ et $DD'$ sont concourantes.

Rapport anharmonique sur un cercle

Lorsque quatre points $A, B, C, D$ appartiennent à un même cercle, on peut parler de leur rapport anharmonique $(A,B;C,D)$ grâce à la propriété suivante :

Proposition (définition du rapport anharmonique de $4$ points cocycliques)
Soit $A, B, C, D$ quatre points sur un même cercle, et $P$ un cinquième point sur le cercle. Alors le rapport anharmonique $(PA, PB; PC, PD)$ ne dépend pas du point $P$ choisi. On parle alors du rapport anharmonique des quatre points cocycliques $A, B, C, D$.

Démonstration
Le sinus de $\widehat{APC}$ ne dépend pas de $P$ lorsque $P$ varie sur le cercle. Il en est de même pour $\sin \widehat{APD}$, $\sin \widehat{BPC}$ et $\sin \widehat{BPD}$, de sorte que la formule que nous avons vue avec les sinus donne toujours la même valeur pour $(PA, PB; PC, PD)$.

Théorème de Pascal

Le théorème de Pascal s'énonce comme suit, et possède une démonstration très simple en utilisant les rapports anharmoniques.

Théorème de Pascal
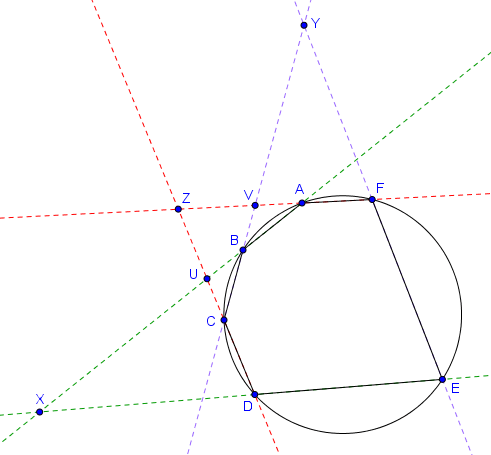
Soit $ABCDEF$ un hexagone inscrit dans un cercle, dont les côtés opposés ne sont pas parallèles. Désignons par $X$ l'intersection des côtés opposés $AB$ et $DE$, par $Y$ l'intersection des côtés opposés $BC$ et $EF$, et par $Z$ l'intersection des côtés opposés $CD$ et $FA$. Alors $X$, $Y$ et $Z$ sont alignés.


Démonstration
Le rapport anharmonique des quatre points cocycliques $A, E, C, B$ est à la fois égal à $(DA, DE; DC, DB)$ et à $(FA, FE; FC, FB)$. En considérant la droite $AB$ qui est sécante aux quatre droites $DA$, $DE$, $DC$ et $DB$, on trouve que $(DA, DE; DC, DB) = (A,X;U,B)$. D'autre part, en considérant la droite $BC$ qui est sécante aux quatre droites $FA$, $FE$, $FC$ et $FB$, on trouve que $(FA, FE; FC, FB) = (V,Y;C,B)$. On déduit des égalités obtenues que
$$(A,X;U,B) = (V,Y;C,B).$$ Le point $B$ est commun à ces deux rapports anharmoniques. Il découle donc de la propriété vue plus haut que les droites $AV$, $XY$ et $UC$ sont concourantes. Mais $AV$ et $UC$ s'intersectent en $Z$, donc cela signifie que $X$, $Y$ et $Z$ sont alignés.

Le théorème de Pascal tel qu'énoncé ci-dessus possède en fait une réciproque : si un hexagone est tel que les intersections des côtés opposés sont alignées, alors l'hexagone est inscrit dans une conique. Cela dépasse cependant le cadre de ce site : on s'intéresse rarement aux coniques autres que les cercles (et il n'est pas nécessaire de savoir ce qu'on entend par conique ici).

Théorème de Pappus

Le théorème de Pappus est très similaire au théorème de Pascal, sauf qu'au lieu d'avoir six points sur un cercle, on a trois points sur une droite et trois autres sur une autre droite. En fait, ces deux droites peuvent être vues comme une conique dégénérée (voir remarque précédente), mais ce n'est pas important pour nous.

Théorème de Pappus
Soit $A, B, C$ trois points alignés, et $A', B', C'$ trois autres points alignés. Désignons par $X$ l'intersection de $BC'$ et $B'C$, par $Y$ l'intersection de $AC'$ et $A'C$, et par $Z$ l'intersection de $AB'$ et $A'B$ (pourvu qu'elles existent). Alors $X$, $Y$ et $Z$ sont alignés.


Démonstration
Nous donnons la démonstration dans le cas où les deux droites définies par $A, B, C$ et $A', B', C'$ sont sécantes en un point $P$. Dans la preuve du théorème de Pascal, on remplace les points $A, B, C, D, E, F$ par les points $A, B', C, A', B, C'$ respectivement. Pour que la même preuve donne le résultat, il suffit alors de voir que
$$(A'A, A'B; A'C, A'B') = (C'A, C'B; C'C, C'B'),$$ qui constituait la première étape de la preuve. Or on voit facilement que les quatre droites $A'A$, $A'B$, $A'C$ et $A'B'$ intersectent la droite définie par $A, B, C$ en les points $A$, $B$, $C$ et $P$ respectivement. Et il en est de même pour les quatre droites $C'A$, $C'B$, $C'C$ et $C'B'$, donc dans les deux cas la valeur du rapport anharmonique des quatre droites est $(A, B; C, P)$.

Dans les théorèmes de Pascal et de Pappus, on suppose que les intersections existent toujours. Nous allons voir dans la partie "plan projectif réel" de ce chapitre que ces conditions ne sont en fait pas nécessaires et que les théorèmes restent vrais dans les cas dégénérés.