Théorie > Géométrie > Rapports anharmoniques
Dans la nature
Des divisions harmoniques apparaissent naturellement dans diverses situations.
Dans un triangle $ABC$, on peut prendre $d = AB$ et $d' = AC$, et le résultat nous indique que la bissectrice extérieure de $\hat A$ est conjuguée harmonique de la bissectrice intérieure de $\hat A$ par rapport aux deux côtés $AB$ et $AC$. Si $|AB| \neq |AC|$ et si $X$ (respectivement $Y$) désigne l'intersection de la bissectrice intérieure (respectivement extérieure) de $\hat A$ avec $BC$, on en déduit que $X, Y, B, C$ forment une division harmonique. Pour ceux ayant vu la théorie des cercles d'Apollonius, on peut voir ici un lien clair : on sait que les points $X$ et $Y$ appartiennent au $A$-cercle d'Apollonius, et la définition de ce cercle donne immédiatement que $X$ et $Y$ sont conjugués harmoniques par rapport à $B,C$.
Le lecteur averti aura deviné l'énoncé de la propriété suivante :
Il s'avère alors que chacune des trois diagonales est coupée harmoniquement par les deux autres :
Il est aussi possible de prouver la propriété ci-dessus en utilisant les théorèmes de Ceva et Ménélaüs. Mais il est également possible d'utiliser cette propriété pour démontrer Ceva à partir de Ménélaüs (ou le contraire).
$$\frac{|GO|}{|GE|} = \frac {2x}{x} = 2\quad \text{ et }\quad \frac{|HO|}{|HE|} = \frac{|GH|+|GO|}{|GH|-|GE|} = \frac{6x}{3x} = 2,$$ ce qui montre que $(G,H;O,E) = -1$.
Bissectrices intérieures et extérieures
La première illustration est très simple :Propriété (bissectrices)
Si $d$ et $d'$ sont deux droites sécantes, alors les deux bissectrices des angles qu'elles forment sont conjuguées harmoniques par rapport à $d, d'$.
Démonstration
Cela découle directement de la formule vue précédemment donnant le rapport anharmonique de $4$ droites en fonction des sinus des angles qu'elles forment entre elles.
Dans un triangle $ABC$, on peut prendre $d = AB$ et $d' = AC$, et le résultat nous indique que la bissectrice extérieure de $\hat A$ est conjuguée harmonique de la bissectrice intérieure de $\hat A$ par rapport aux deux côtés $AB$ et $AC$. Si $|AB| \neq |AC|$ et si $X$ (respectivement $Y$) désigne l'intersection de la bissectrice intérieure (respectivement extérieure) de $\hat A$ avec $BC$, on en déduit que $X, Y, B, C$ forment une division harmonique. Pour ceux ayant vu la théorie des cercles d'Apollonius, on peut voir ici un lien clair : on sait que les points $X$ et $Y$ appartiennent au $A$-cercle d'Apollonius, et la définition de ce cercle donne immédiatement que $X$ et $Y$ sont conjugués harmoniques par rapport à $B,C$.
Tangentes à deux cercles
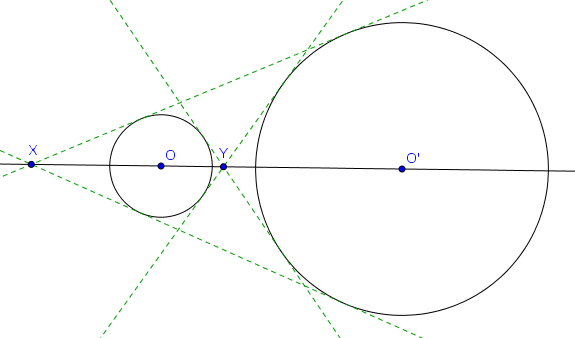
Considérons maintenant une toute autre situation : deux cercles $\mathcal{C}$ et $\mathcal{C}'$ extérieurs l'un à l'autre, de centres $O$ et $O'$ et de rayons différents. On dessine les quatre droites qui sont tangentes aux deux cercles, et on considère les intersections $X, Y$ qui se situent sur $OO'$ (voir figure ci-dessous).
Le lecteur averti aura deviné l'énoncé de la propriété suivante :
Propriété (tangentes à deux cercles)
Dans la configuration ci-dessus, les points $X$ et $Y$ sont conjugués harmoniques par rapport à $O, O'$, autrement dit $(X,Y;O,O') = -1$.
Démonstration
En considérant les points de tangences des droites considérées avec les deux cercles, on s'aperçoit immédiatement par triangles semblables que $\frac{|XO|}{|XO'|} = \frac{R}{R'}$ où $R$ et $R'$ sont les rayons des cercles $\mathcal{C}$ et $\mathcal{C}'$. De la même façon on obtient que $\frac{|YO|}{|YO'|} = \frac{R}{R'}$ également. Cela montre que $(X,Y;O,O') = -1$ (par la définition du rapport anharmonique de ces quatre points).
Quadrilatère complet
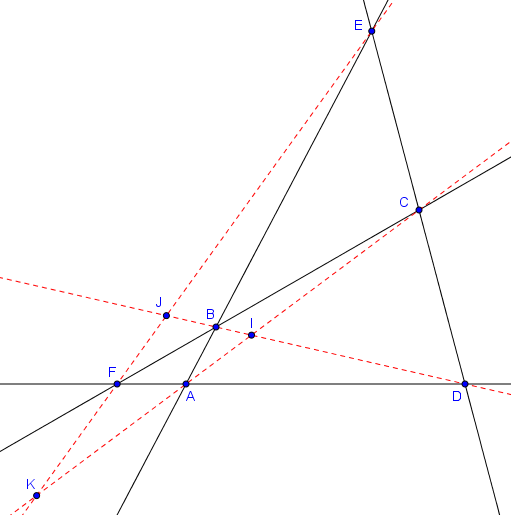
Un quadrilatère complet est un quadrilatère convexe $ABCD$ dont les côtés ne sont pas parallèles et auquel on ajoute l'intersection $E$ de $AB$ et $CD$ et l'intersection $F$ de $BC$ et $DA$, comme sur la figure ci-dessous. Une droite reliant deux des points $A, B, C, D, E, F$ et qui n'est pas déjà dessinée est alors appelée une diagonale du quadrilatère complet. Il y a trois diagonales : $AC$, $BD$ et $EF$.
Il s'avère alors que chacune des trois diagonales est coupée harmoniquement par les deux autres :
Proposition (quadrilatère complet)
Soit $A,B,C,D,E,F$ six points formant un quadrilatère complet comme ci-dessus. Désignons par $I$ l'intersection de $AC$ et $BD$, par $J$ l'intersection de $BD$ et $EF$, et par $K$ l'intersection de $EF$ et $AC$. Alors $(I,J;B,D) = -1$, $(J,K;E,F) = -1$ et $(K,I;A,C) = -1$.
Démonstration
Nous allons prouver que $(I,J,B,D) = -1$, les autres égalités ayant des preuves similaires.
Nous devons montrer que $I, J, B, D$ forment une division harmonique, et nous allons en fait montrer que les droites $EI$, $EJ$, $EB$, $ED$ forment un faisceau harmonique. Pour cela, considérons la droite $d$ passant par $E$ qui est la conjuguée harmonique de $EJ$ par rapport à $EB$ et $ED$. Il s'agirait de montrer que $d$ n'est autre que $EI$. Notons $X$ l'intersection de $d$ avec $BC$ et $Y$ l'intersection de $d$ avec $AD$. Comme les droites $d$, $EJ$, $EB$, $ED$ forment un faisceau harmonique, on déduit que $(X,F;B,C) = -1$ et $(Y,F;A,D) = -1$. Donc $(IX, IF; IB, IC) = -1$ et $(IY, IF; IA, ID) = -1$. La première égalité signifie que $IX$ est conjuguée harmonique de $IF$ par rapport à $IB, IC$, et la deuxième que $IY$ est conjuguée harmonique de $IF$ par rapport à $IA, ID$. Mais les paires $IB, IC$ et $IA, ID$ sont les mêmes, donc $IX$ et $IY$ sont toutes deux conjuguées harmoniques de $IF$ par rapport à la même paire de droite. Par unicité du conjugué harmonique, on en déduit que $IX = IY$, autrement dit $I$ se situe sur $XY = d$ comme voulu.
Nous devons montrer que $I, J, B, D$ forment une division harmonique, et nous allons en fait montrer que les droites $EI$, $EJ$, $EB$, $ED$ forment un faisceau harmonique. Pour cela, considérons la droite $d$ passant par $E$ qui est la conjuguée harmonique de $EJ$ par rapport à $EB$ et $ED$. Il s'agirait de montrer que $d$ n'est autre que $EI$. Notons $X$ l'intersection de $d$ avec $BC$ et $Y$ l'intersection de $d$ avec $AD$. Comme les droites $d$, $EJ$, $EB$, $ED$ forment un faisceau harmonique, on déduit que $(X,F;B,C) = -1$ et $(Y,F;A,D) = -1$. Donc $(IX, IF; IB, IC) = -1$ et $(IY, IF; IA, ID) = -1$. La première égalité signifie que $IX$ est conjuguée harmonique de $IF$ par rapport à $IB, IC$, et la deuxième que $IY$ est conjuguée harmonique de $IF$ par rapport à $IA, ID$. Mais les paires $IB, IC$ et $IA, ID$ sont les mêmes, donc $IX$ et $IY$ sont toutes deux conjuguées harmoniques de $IF$ par rapport à la même paire de droite. Par unicité du conjugué harmonique, on en déduit que $IX = IY$, autrement dit $I$ se situe sur $XY = d$ comme voulu.
Il est aussi possible de prouver la propriété ci-dessus en utilisant les théorèmes de Ceva et Ménélaüs. Mais il est également possible d'utiliser cette propriété pour démontrer Ceva à partir de Ménélaüs (ou le contraire).
Droite d'Euler
Dans le chapitre sur les transformations du plan, nous avons vu que la droite d'Euler d'un triangle est une droite particulière passant par le centre du cercle circonscrit $O$, l'orthocentre $H$, le centre de gravité $G$, mais aussi le centre du cercle d'Euler $E$. En fait, il s'avère que les points $G$, $H$, $O$, $E$ forment une division harmonique ! En effet, si on note $x = |GE|$, alors nous avons vu dans le chapitre en question que $|GO| = 2 \cdot |GE| = 2x$ et $|HG| = 2 \cdot |GO| = 4x$. Nous avons donc$$\frac{|GO|}{|GE|} = \frac {2x}{x} = 2\quad \text{ et }\quad \frac{|HO|}{|HE|} = \frac{|GH|+|GO|}{|GH|-|GE|} = \frac{6x}{3x} = 2,$$ ce qui montre que $(G,H;O,E) = -1$.