Concours > Concours #19

Description

Pendant que les athlètes français récoltent une moisson de médailles à Paris, à votre tour d’essayer d’obtenir une médaille dans ce nouveau concours, baptisé le concours des JO ! N’hésitez pas à tenter votre chance face aux 9 problèmes insolites et variés que nous allons vous proposer !

Les problèmes seront décomposés en trois séries de trois problèmes. Au sein de chaque série, les problèmes sont par ordre croissant de difficulté, le premier problème étant toujours très accessible. Chaque série sera disponible pendant deux jours seulement. De plus, la première série de problèmes sera bien plus abordable que les deux suivantes. Vous l’aurez compris, seuls de rares quoicouchads pourront parvenir à résoudre le dernier problème des deux dernières séries… Enfin, nous avons fait en sorte que tous les thèmes apparaissent de façon équitable parmi les 9 problèmes, pour éviter les jaloux !

Alors n’hésitez pas, venez vous frotter à nos problèmes si vous n’avez pas peur de vous y casser les dents 3:[

Organisateurs du concours : 3Anatole Bouton, 4Erik D., 8Noé Fisher, Aurélien Fourré, Youssef G. et 5Solal Pivron-Djeddi.

Problème #1

Solutions acceptées du lundi 5 août 2024 à 12h00 au mercredi 7 août 2024 à 12h00 (heures belges).
Énoncé
Teddy écrit $n \geq 2$ nombres réels strictement positifs non nécessairement distincts sur son tatami. Il remarque que quel que soit le nombre qu'il efface, la somme des $n-1$ nombres restants est toujours entière. Montrer que tous les nombres écrits par Teddy sont rationnels.
Statistiques
Tenté par 293 personnes
Scores parfaits : 245
Origine du problème : Création originale (Anatole Bouton)

Problème #2

Solutions acceptées du lundi 5 août 2024 à 12h00 au mercredi 7 août 2024 à 12h00 (heures belges).
Énoncé
Antoine veut jouer avec ses $1+2+3+\ldots+4242$ ballons de rugby. Il les dispose pour cela en $4242$ lignes, la $i$-ème ligne contenant $i$ ballons espacés de $1$ mètre en $1$ mètre, afin de former un grand triangle équilatéral. Il veut ensuite enlever certains de ces ballons afin que trois ballons restants ne forment jamais un triangle équilatéral de côté $1$ mètre. Combien de ballons doit il enlever, au minimum ?

Par exemple, si Antoine décidait de jouer avec $1+2+3+4+5+6 = 21$ ballons pour former un grand triangle équilatéral de taille $6$, voici comment il les disposerait :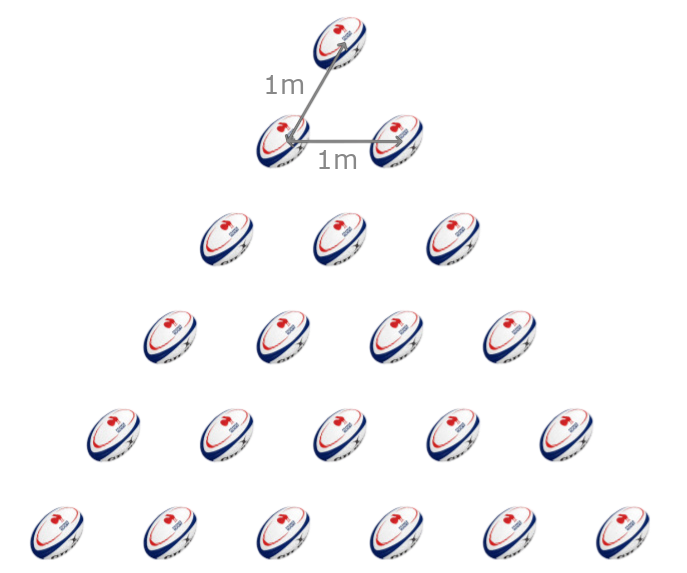

Statistiques
Tenté par 163 personnes
Scores parfaits : 52
Origine du problème : Création originale (Anatole Bouton)

Problème #3

Solutions acceptées du lundi 5 août 2024 à 12h00 au mercredi 7 août 2024 à 12h00 (heures belges).
Énoncé
Trouver toutes les suites $(u_n)_{n\in\mathbb N}$ d'entiers strictement positifs telles que, pour tout $n\in\mathbb N$, $$u_n \mid 2^{u_{n+1}}-1$$
Statistiques
Tenté par 176 personnes
Scores parfaits : 64
Origine du problème : Création originale (Anatole Bouton)

Problème #4

Solutions acceptées du mercredi 7 août 2024 à 12h00 au vendredi 9 août 2024 à 12h00 (heures belges).
Énoncé
Soit $\Omega$ un cercle et $\gamma_1$, $\gamma_2$ deux cercles tangents intérieurement à $\Omega$ en $P$ et $Q$ respectivement. On suppose de plus que $\gamma_1$ et $\gamma_2$ sont tangents extérieurement en $T$. Montrer que la perpendiculaire à la droite $(PT)$ passant par $P$ intersecte la droite $(QT)$ sur $\Omega$.
Statistiques
Tenté par 106 personnes
Scores parfaits : 75
Origine du problème : Cut The Knot

Problème #5

Solutions acceptées du mercredi 7 août 2024 à 12h00 au vendredi 9 août 2024 à 12h00 (heures belges).
Énoncé
Trouver tous les couples $((b_n)_{n\in\mathbb N},(c_n)_{n\in\mathbb N})$ de suites réelles telles que pour tout $n\in\mathbb N$, $b_n\le c_n$ et $b_{n+1},c_{n+1}$ sont les deux solutions de l'équation $x^2+b_nx+c_n=0$.
Statistiques
Tenté par 101 personnes
Scores parfaits : 37
Origine du problème : 2020 China Girls Math Olympiad, Problème 5

Problème #6

Solutions acceptées du mercredi 7 août 2024 à 12h00 au vendredi 9 août 2024 à 12h00 (heures belges).
Énoncé
On considère une grille infinie composée de carrés unités. Un polygone olympique est un polygone qui ne s'auto-intersecte pas et dont les côtés suivent les lignes de la grille.
Sara et Manon jouent à un jeu. Sara choisit d'abord un polygone olympique $P$, puis Manon colore certains carrés unités de la grille en bleu, afin que tout polygone olympique obtenu par translation et/ou rotation de $P$ contienne entre $1$ et $2024$ cases bleues (inclus).
Sara peut-elle choisir son polygone afin de rendre la tâche de Manon impossible ?
Statistiques
Tenté par 31 personnes
Scores parfaits : 0
Origine du problème : USEMO 2019, Problème 3

Problème #7

Solutions acceptées du vendredi 9 août 2024 à 12h00 au dimanche 11 août 2024 à 12h00 (heures belges).
Énoncé
Soit $0 < a_{1} < a_{2} <\dots$ une suite infinie strictement croissante d'entiers strictement positifs. On suppose qu'il existe un entier $k$ tel que pour tout entier $n\geq k$, $a_n$ est la somme de deux autres termes, non nécessairement distincts, de la suite. Montrer que la suite contient une infinité de nombres composés.
Statistiques
Tenté par 116 personnes
Scores parfaits : 80
Origine du problème : 2015 Bulgaria EGMO TST, Problème 1

Problème #8

Solutions acceptées du vendredi 9 août 2024 à 12h00 au dimanche 11 août 2024 à 12h00 (heures belges).
Énoncé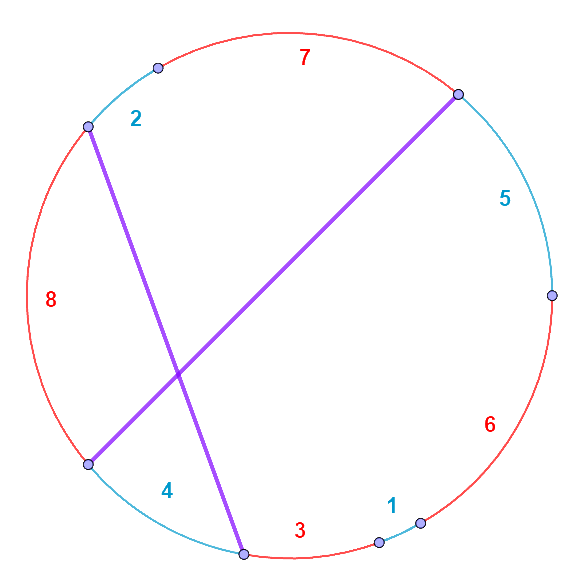
Léon répartit $100$ de ses médailles (d'or) sur un cercle de circonférence $1+2+\dots+100$ mètres de sorte à ce que les longueurs en mètres des $100$ arcs qu'elles déterminent décrivent les entiers de $1$ à $100$, dans un certain ordre. Montrer qu'il existe deux cordes perpendiculaires du cercle dont les extrémités sont des médailles.
Statistiques
Tenté par 52 personnes
Scores parfaits : 2
Origine du problème : Tot Fall 2011, Problème A7

Problème #9

Solutions acceptées du vendredi 9 août 2024 à 12h00 au dimanche 11 août 2024 à 12h00 (heures belges).
Énoncé
Soit $ABC$ un triangle acutangle et $O$ le centre de son cercle circonscrit. Soit $\gamma_B$ et $\gamma_C$ les cercles inscrits aux triangles $AOC$ et $AOB$ respectivement. On suppose que les tangentes communes extérieures aux cercles $\gamma_B$ et $\gamma_C$ coupent la droite $(BC)$ en les points $M$ et $N$. Montrer que les cercles circonscrits aux triangles $ABC$ et $AMN$ sont tangents.
Statistiques
Tenté par 17 personnes
Scores parfaits : 0
Origine du problème : AOPS