Théorie > Inégalités > Introduction aux inégalités
Prérequis
Aucun prérequis.
Résumé
Nous expliquons dans ce premier chapitre le principe des problèmes d'inégalités. Nous donnons également les résultats basiques permettant de manipuler les inégalités correctement ainsi que les inégalités relatives aux polynômes du second degré. Ce sont ces dernières qui sont à la base de la plupart des inégalités remarquables présentées dans la suite du cours.
Ce chapitre a été écrit par B. Legat et N. Radu et mis en ligne le 8 décembre 2014.
1. Principe
Les problèmes d'inégalités se ressemblent tous. L'énoncé typique d'un tel problème est le suivant.
On doit donc généralement montrer une certaine inégalité contenant des variables sur lesquelles on a éventuellement des conditions (ici, $xyz=1$).
Pour résoudre une inégalité, il faut tout d'abord connaître des inégalités remarquables. Nous verrons tout au long de ce cours les inégalités de Cauchy-Schwarz, de Jensen, de Minkowski, de Tchebychev, et bien d'autres. Il s'agit ensuite d'utiliser certaines de ces inégalités pour montrer celle qui nous intéresse. Un problème ne consiste évidemment jamais à uniquement utiliser une inégalité remarquable : il faut souvent effectuer des changements de variables ou utiliser des astuces pour simplifier l'inégalité que l'on désire montrer.
Nous allons voir les différentes techniques qui permettent généralement de résoudre un tel problème. C'est ensuite comme toujours une question d'entraînement !
Problème (IMO 2008, Problème 2)
Si $x$, $y$ et $z$ sont des nombres réels, tous différents de $1$ mais tels que $xyz=1$, alors montrer que
$$\frac{x^2}{(x-1)^2} + \frac{y^2}{(y-1)^2} + \frac{z^2}{(z-1)^2} \geq 1.$$
$$\frac{x^2}{(x-1)^2} + \frac{y^2}{(y-1)^2} + \frac{z^2}{(z-1)^2} \geq 1.$$
On doit donc généralement montrer une certaine inégalité contenant des variables sur lesquelles on a éventuellement des conditions (ici, $xyz=1$).
Pour résoudre une inégalité, il faut tout d'abord connaître des inégalités remarquables. Nous verrons tout au long de ce cours les inégalités de Cauchy-Schwarz, de Jensen, de Minkowski, de Tchebychev, et bien d'autres. Il s'agit ensuite d'utiliser certaines de ces inégalités pour montrer celle qui nous intéresse. Un problème ne consiste évidemment jamais à uniquement utiliser une inégalité remarquable : il faut souvent effectuer des changements de variables ou utiliser des astuces pour simplifier l'inégalité que l'on désire montrer.
Nous allons voir les différentes techniques qui permettent généralement de résoudre un tel problème. C'est ensuite comme toujours une question d'entraînement !
2. Manipulation d'inégalités
Lorsque l'on est en présence d'une inégalité du type
$$\left(\frac{x+y}{x^2+1}\right)^3 \leq \left( \frac{x-y}{x^2+1} \right)^3,$$ il est naturel de se demander comment elle peut être simplifiée. Peut-on appliquer la racine cubique des deux côtés de l'inégalité ? Peut-on ensuite multiplier les deux membres par $x^2+1$ ? C'est à ces questions élémentaires que nous répondons ici.
Nous donnons en fait quelques résultats basiques concernant les inégalités permettant de les manipuler. Ceux-ci peuvent paraître élémentaires mais toute la difficulté réside dans leur utilisation. En effet, les nombres réels $a$, $b$, $c$, $d$ et $k$ intervenant dans les prochaines inégalités seront dans la pratique remplacés par des expressions réelles plus complexes.
Il faut faire très attention au sens de l'implication.
En effet, si on sait que $a + b \leq c + d$ et que $a \leq c$, alors on ne peut pas forcément conclure que $b \leq d$. On a par exemple $1+4 \leq 3+3$ et $1 \leq 3$ alors que $4 \not \leq 3$.
La plupart du temps, on multiplie (à raison) les deux côtés d'une inégalité par un nombre positif. Il ne faut cependant pas oublier que si on la multiplie par un nombre négatif, l'inégalité s'inverse.
En général, lorsqu'on applique une transformation des deux côtés d'une inégalité, il faut vérifier que la fonction que l'on applique est croissante ou décroissante. D'ailleurs, on remarque que la fonction $f(x) = kx$ est strictement croissante pour $k > 0$ et strictement décroissante pour $k < 0$, ce qui fait de la multiplication par un scalaire un cas particulier des résultats précédents.
Le sens de l'implication est aussi très important ici. Si on veut prouver une inégalité $a \leq b$ et qu'on trouve que $f(a) \leq f(b)$, il faut la croissance stricte de $f$ pour pouvoir conclure. En effet, il se peut dans le cas contraire que $f$ soit constante sur un intervalle et qu'on ait $a > b$ avec $f(a) = f(b)$.
$$\left(\frac{x+y}{x^2+1}\right)^3 \leq \left( \frac{x-y}{x^2+1} \right)^3,$$ et regardons comment celle-ci peut-être simplifiée.
La fonction $f : x \mapsto x^3$ étant strictement croissante, on peut directement dire que cette inégalité est équivalente à
$$\frac{x+y}{x^2+1} \leq \frac{x-y}{x^2+1}.$$ Ensuite, vu qu'on a clairement $x^2+1 \geq 1 > 0$ pour tout $x \in \mathbb{R}$, on peut multiplier les deux membres de cette dernière inégalité par $x^2+1$ sans que le sens de celle-ci soit inversé, pour obtenir
$$x+y \leq x-y.$$ Comme pour les égalités, on peut bien sûr faire passer les termes d'un membre à l'autre, et notre inégalité est finalement équivalente à
$$2y \leq 0.$$ On en déduit que l'inégalité de départ est vraie si et seulement si $y$ est négatif (et $x$ est quelconque).
$$\left(\frac{x+y}{x^2+1}\right)^3 \leq \left( \frac{x-y}{x^2+1} \right)^3,$$ il est naturel de se demander comment elle peut être simplifiée. Peut-on appliquer la racine cubique des deux côtés de l'inégalité ? Peut-on ensuite multiplier les deux membres par $x^2+1$ ? C'est à ces questions élémentaires que nous répondons ici.
Nous donnons en fait quelques résultats basiques concernant les inégalités permettant de les manipuler. Ceux-ci peuvent paraître élémentaires mais toute la difficulté réside dans leur utilisation. En effet, les nombres réels $a$, $b$, $c$, $d$ et $k$ intervenant dans les prochaines inégalités seront dans la pratique remplacés par des expressions réelles plus complexes.
Combinaison de deux inégalités
Lemme
Pour tous $a,b,c,d \in \mathbb{R}$,
\[ a \leq c \ \text{ et } \ b \leq d \Rightarrow a + b \leq c + d. \]
\[ a \leq c \ \text{ et } \ b \leq d \Rightarrow a + b \leq c + d. \]
Il faut faire très attention au sens de l'implication.
En effet, si on sait que $a + b \leq c + d$ et que $a \leq c$, alors on ne peut pas forcément conclure que $b \leq d$. On a par exemple $1+4 \leq 3+3$ et $1 \leq 3$ alors que $4 \not \leq 3$.
Multiplication par un scalaire
Lemme
Pour tous $a,b \in \mathbb{R}$ et $k \in \mathbb{R}^+_0$,
\[ a \leq b \Leftrightarrow ak \leq bk. \]
\[ a \leq b \Leftrightarrow ak \leq bk. \]
Lemme
Pour tous $a,b \in \mathbb{R}$ et $k \in \mathbb{R}^-_0$,
\[ a \leq b \Leftrightarrow ak \geq bk. \]
\[ a \leq b \Leftrightarrow ak \geq bk. \]
La plupart du temps, on multiplie (à raison) les deux côtés d'une inégalité par un nombre positif. Il ne faut cependant pas oublier que si on la multiplie par un nombre négatif, l'inégalité s'inverse.
Application d'une fonction
Lemme
Soit $f:A\to\mathbb{R}$ une fonction croissante sur $B \subseteq A$.
Pour tous $a,b \in B$,
\[ a \leq b \Rightarrow f(a) \leq f(b). \] Si $f$ est strictement croissante, c'est un $\Leftrightarrow$.
Pour tous $a,b \in B$,
\[ a \leq b \Rightarrow f(a) \leq f(b). \] Si $f$ est strictement croissante, c'est un $\Leftrightarrow$.
Lemme
Soit $f:A\to\mathbb{R}$ une fonction décroissante sur $B \subseteq A$.
Pour tous $a,b \in B$,
\[ a \leq b \Rightarrow f(a) \geq f(b). \] Si $f$ est strictement décroissante, c'est un $\Leftrightarrow$.
Pour tous $a,b \in B$,
\[ a \leq b \Rightarrow f(a) \geq f(b). \] Si $f$ est strictement décroissante, c'est un $\Leftrightarrow$.
En général, lorsqu'on applique une transformation des deux côtés d'une inégalité, il faut vérifier que la fonction que l'on applique est croissante ou décroissante. D'ailleurs, on remarque que la fonction $f(x) = kx$ est strictement croissante pour $k > 0$ et strictement décroissante pour $k < 0$, ce qui fait de la multiplication par un scalaire un cas particulier des résultats précédents.
Le sens de l'implication est aussi très important ici. Si on veut prouver une inégalité $a \leq b$ et qu'on trouve que $f(a) \leq f(b)$, il faut la croissance stricte de $f$ pour pouvoir conclure. En effet, il se peut dans le cas contraire que $f$ soit constante sur un intervalle et qu'on ait $a > b$ avec $f(a) = f(b)$.
Retour à l'exemple
Considérons à nouveau l'inégalité$$\left(\frac{x+y}{x^2+1}\right)^3 \leq \left( \frac{x-y}{x^2+1} \right)^3,$$ et regardons comment celle-ci peut-être simplifiée.
La fonction $f : x \mapsto x^3$ étant strictement croissante, on peut directement dire que cette inégalité est équivalente à
$$\frac{x+y}{x^2+1} \leq \frac{x-y}{x^2+1}.$$ Ensuite, vu qu'on a clairement $x^2+1 \geq 1 > 0$ pour tout $x \in \mathbb{R}$, on peut multiplier les deux membres de cette dernière inégalité par $x^2+1$ sans que le sens de celle-ci soit inversé, pour obtenir
$$x+y \leq x-y.$$ Comme pour les égalités, on peut bien sûr faire passer les termes d'un membre à l'autre, et notre inégalité est finalement équivalente à
$$2y \leq 0.$$ On en déduit que l'inégalité de départ est vraie si et seulement si $y$ est négatif (et $x$ est quelconque).
3. Carrés
L'inégalité suivante ne devrait dérouter personne (et on l'a d'ailleurs déjà utilisée sans le mentionner précédemment).
Bien qu'elle soit évidente, elle est une arme redoutable et peut résoudre beaucoup de problèmes si elle est bien utilisée. La difficulté réside généralement dans la factorisation des expressions pour se ramener à une somme de carrés.
Nous verrons par la suite différentes inégalités remarquables qui pourront être utilisées dans la résolution de problèmes. L'ingrédient essentiel à la démonstration de ces inégalités sera en fait à chaque fois l'inégalité $a^2 \geq 0$.
Lemme
Pour tout $a \in \mathbb{R}$, on a
\[ a^2 \geq 0 \] avec égalité si et seulement si $a = 0$.
\[ a^2 \geq 0 \] avec égalité si et seulement si $a = 0$.
Bien qu'elle soit évidente, elle est une arme redoutable et peut résoudre beaucoup de problèmes si elle est bien utilisée. La difficulté réside généralement dans la factorisation des expressions pour se ramener à une somme de carrés.
Nous verrons par la suite différentes inégalités remarquables qui pourront être utilisées dans la résolution de problèmes. L'ingrédient essentiel à la démonstration de ces inégalités sera en fait à chaque fois l'inégalité $a^2 \geq 0$.
4. Second degré
On peut étudier en toute généralité le signe d'un polynôme du second degré. Cette matière va sembler évidente à ceux qui l'ont déjà vue en secondaire, ce qui est normal.
Un polynôme du second degré est une expression de la forme $ax^2 + bx + c$ où $a,b$ et $c$ sont des constantes réelles. On demande aussi généralement que $a \neq 0$ puisque si $a = 0$, alors on a simplement l'expression $bx + c$ qui est bien plus simple à étudier.
Au vu de la formule pour $x_1$ et $x_2$, on comprend mieux pourquoi il n'y a pas de racines réelles quand $b^2 - 4ac < 0$ et pourquoi il n'y a qu'une seule racine lorsque $b^2 - 4ac = 0$.
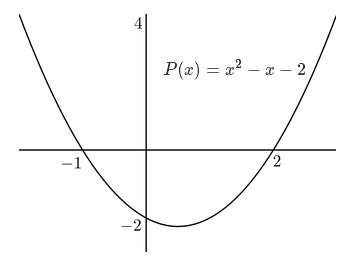
Prenons par exemple le polynôme $P(x) = x^2 - x - 2$. On a $b^2 - 4ac = (-1)^2 - 4(-2) = 9 > 0$ et on est donc dans ce cas dans la dernière configuration du résultat. On calcule aisément $x_1 = -1$ et $x_2 = 2$. Le polynôme est donc du même signe que $a$, c'est à dire positif, pour $x \leq x_1 = -1$ et pour $x \geq x_2 = 2$. Le graphe de cette fonction est le suivant :
$$x^2+y^2+4x+4 \geq y(2x+4).$$ On peut ici penser à $x$ comme étant un simple paramètre, et l'inégalité n'est alors rien d'autre qu'une inégalité impliquant un polynôme du second degré en $y$ :
$$y^2 - (2x+4)y + x^2+4x+4 \geq 0$$ On calcule alors le discriminant $b^2-4ac$ : il vaut ici $(2x+4)^2 - 4(x^2+4x+4) = 0$, ce qui signifie que ce polynôme en $y$ est toujours du signe de $a$, c'est-à-dire positif comme voulu. Notre exemple n'était ici pas très compliqué (on peut en fait remarquer qu'il s'agit simplement de l'inégalité $(x-y+2)^2 \geq 0$), mais cette méthode peut fonctionner dans des cas plus complexes. Il faudra alors discuter les différents cas selon le signe du discriminant.
Un polynôme du second degré est une expression de la forme $ax^2 + bx + c$ où $a,b$ et $c$ sont des constantes réelles. On demande aussi généralement que $a \neq 0$ puisque si $a = 0$, alors on a simplement l'expression $bx + c$ qui est bien plus simple à étudier.
Proposition
Soient $a, b, c \in \mathbb{R}$ avec $a \neq 0$ et $P(x) = ax^2 + bx + c$.
- Si $b^2 - 4ac < 0$, alors $P(x)$ est du signe de $a$ pour tout $x \in \mathbb{R}$ et ne s'annule jamais;
- Si $b^2 - 4ac = 0$, alors $P(x)$ est du signe de $a$ pour tout $x \in \mathbb{R}$ et s'annule en $\frac{-b}{2a}$;
- Si $b^2 - 4ac > 0$, alors $P(x)$ s'annule en deux points $x_1 < x_2$ qui sont appelés ses racines et il est du signe de $a$ pour $x \in \ \left]-\infty, x_1\right[\ \cup \ \left]x_2, +\infty\right[$ et du signe opposé pour tout $x \in \ ]x_1, x_2[$.
Les racines $x_1$ et $x_2$ sont données (éventuellement dans l'ordre inverse lorsque $a < 0$) par
$$\frac{-b - \sqrt{b^2 - 4ac}}{2a} \quad \text{et} \quad \frac{-b + \sqrt{b^2 - 4ac}}{2a}.$$
Au vu de la formule pour $x_1$ et $x_2$, on comprend mieux pourquoi il n'y a pas de racines réelles quand $b^2 - 4ac < 0$ et pourquoi il n'y a qu'une seule racine lorsque $b^2 - 4ac = 0$.
Prenons par exemple le polynôme $P(x) = x^2 - x - 2$. On a $b^2 - 4ac = (-1)^2 - 4(-2) = 9 > 0$ et on est donc dans ce cas dans la dernière configuration du résultat. On calcule aisément $x_1 = -1$ et $x_2 = 2$. Le polynôme est donc du même signe que $a$, c'est à dire positif, pour $x \leq x_1 = -1$ et pour $x \geq x_2 = 2$. Le graphe de cette fonction est le suivant :

Démonstration
L'idée est d'isoler $x$ dans un carré et de ne garder que des constantes à l'extérieur :
$$\begin{align*}
P(x) = ax^2 + bx + c & =
a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a}\\
& =
a\left(\left(x + \frac{b}{2a}\right)^2 + \frac{4ac - b^2}{4a^2}\right).
\end{align*}$$ Pour que $P(x)$ soit du signe de $a$, il faut donc que
$$\left(x + \frac{b}{2a}\right)^2 \geq \frac{b^2 - 4ac}{4a^2}.$$ Le membre de gauche est positif car c'est un carré. Le membre de droite est du signe de $b^2 - 4ac$ car $4a^2 \geq 0$. Dès lors, si $b^2 - 4ac \leq 0$, l'inégalité est vraie pour tout $x$.
Sinon, les deux membres sont positifs. Comme la fonction $f: x \mapsto \sqrt{x}$ est strictement croissante pour $x \in \mathbb{R}^+$, notre inégalité est équivalente à
$$\left|x + \frac{b}{2a}\right| \geq
\frac{\sqrt{b^2 - 4ac}}{2|a|}$$ ce qui est vrai lorsque $x \leq x_1$ ou $x \geq x_2$ où $x_1$ (respectivement $x_2$) est le plus petit (resp. le plus grand) des deux nombres
$$\frac{-b - \sqrt{b^2 - 4ac}}{2a} \quad \text{et} \quad \frac{-b + \sqrt{b^2 - 4ac}}{2a}.$$
$$\begin{align*}
P(x) = ax^2 + bx + c & =
a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a}\\
& =
a\left(\left(x + \frac{b}{2a}\right)^2 + \frac{4ac - b^2}{4a^2}\right).
\end{align*}$$ Pour que $P(x)$ soit du signe de $a$, il faut donc que
$$\left(x + \frac{b}{2a}\right)^2 \geq \frac{b^2 - 4ac}{4a^2}.$$ Le membre de gauche est positif car c'est un carré. Le membre de droite est du signe de $b^2 - 4ac$ car $4a^2 \geq 0$. Dès lors, si $b^2 - 4ac \leq 0$, l'inégalité est vraie pour tout $x$.
Sinon, les deux membres sont positifs. Comme la fonction $f: x \mapsto \sqrt{x}$ est strictement croissante pour $x \in \mathbb{R}^+$, notre inégalité est équivalente à
$$\left|x + \frac{b}{2a}\right| \geq
\frac{\sqrt{b^2 - 4ac}}{2|a|}$$ ce qui est vrai lorsque $x \leq x_1$ ou $x \geq x_2$ où $x_1$ (respectivement $x_2$) est le plus petit (resp. le plus grand) des deux nombres
$$\frac{-b - \sqrt{b^2 - 4ac}}{2a} \quad \text{et} \quad \frac{-b + \sqrt{b^2 - 4ac}}{2a}.$$
Utilisation pratique
Lorsqu'on désire montrer une inégalité avec plusieurs variables, une bonne idée peut-être de n'en considérer qu'une seule comme étant une variable et de voir les autres comme des paramètres. Imaginons par exemple que l'on désire montrer l'inégalité$$x^2+y^2+4x+4 \geq y(2x+4).$$ On peut ici penser à $x$ comme étant un simple paramètre, et l'inégalité n'est alors rien d'autre qu'une inégalité impliquant un polynôme du second degré en $y$ :
$$y^2 - (2x+4)y + x^2+4x+4 \geq 0$$ On calcule alors le discriminant $b^2-4ac$ : il vaut ici $(2x+4)^2 - 4(x^2+4x+4) = 0$, ce qui signifie que ce polynôme en $y$ est toujours du signe de $a$, c'est-à-dire positif comme voulu. Notre exemple n'était ici pas très compliqué (on peut en fait remarquer qu'il s'agit simplement de l'inégalité $(x-y+2)^2 \geq 0$), mais cette méthode peut fonctionner dans des cas plus complexes. Il faudra alors discuter les différents cas selon le signe du discriminant.