Théorie > Fondements > Rédaction d'une preuve

Général
Résumé Chapitre entier
Points théoriques
Conseils généraux Exemple algébrique Exemple géométrique Exemple combinatoire Exercice supplémentaire
Exercices
Exercice 1 Exercice 2

Exemple géométrique

Regardons à présent un problème de géométrie et une solution à celui-ci. Les étapes de la solution sont relativement élémentaires, mais il est possible que vous n'ayez pas encore vu toute la théorie utilisée. Ce n'est pas grave : le principal est surtout de lire les conseils sur la rédaction de la solution.

Problème
Soit $ABC$ un triangle et $\ell$ la tangente en $A$ au cercle circonscrit à $ABC$. Le cercle passant par $A$ et tangent à $BC$ en $B$ (respectivement $C$) coupe $\ell$ en $A$ et $C'$ (respectivement $B'$). Montrer que
$$\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2$$

Solution 1 (mauvaise)
On trouve que $\widehat{ACB} = \widehat{C'AB} = \widehat{AB'C}$ et $\widehat{ABC} = \widehat{B'AC} = \widehat{AC'B}$ par chasse aux angles, donc les triangles $ABC'$ et $ACB'$ sont semblables. Donc $\frac{|C'B|}{|AC|} = \frac{|AB|}{|B'C|}$. Donc $\frac{\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|}}{2} \ge \sqrt{\frac{|B'C|}{|AB|} \cdot \frac{|C'B|}{|AC|}} = 1$ par AM-GM, donc $\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2$.


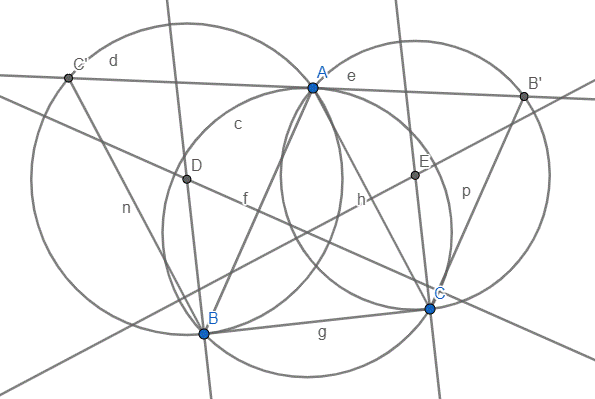
Il y a plein de choses à redire sur cette solution :

  • C'est très bien d'inclure une figure pour un problème de géométrie. Par contre, il faut que cette figure soit lisible ! Ici, la personne écrivant cette solution a laissé sur la figure des droites qu'il a utilisées pour la construire, alors qu'elles sont parfaitement inutiles pour la solution. Il a également laissé les étiquettes de toutes les droites, et il n'a pas fait l'effort de bouger les noms des points intéressants pour les rendre plus faciles à lire. Il est donc presque impossible de se servir de cette figure pour suivre la solution... Une bonne figure devrait aussi mettre en évidence, si possible avec des couleurs, les angles de même amplitude révélés par la chasse aux angles. Un exemple de bonne figure est donné plus bas.

  • La chasse aux angles n'est pas détaillée du tout, et c'est ici au lecteur de se demander comment chaque égalité a été obtenue, ce qui n'est pas évident. Ce qui complexifie encore plus la compréhension, c'est le fait que les égalités d'angles ne sont pas écrites dans le bon ordre ! Ici, les égalités $\widehat{C'AB} = \widehat{ACB}$ et $\widehat{ACB} = \widehat{AB'C}$ sont les égalités que l'on connaît, et on veut en déduire que $\widehat{C'AB} = \widehat{AB'C}$. Dans ce cas, il faut absolument écrire
    $$\widehat{C'AB} = \widehat{ACB} = \widehat{AB'C}$$ pour que chaque signe $=$ corresponde à une égalité connue et que l'égalité démontrée soit celle entre le premier et le dernier terme. Le lecteur lit de gauche à droite, et quand il lit
    $$\widehat{ACB} = \widehat{C'AB} = \widehat{AB'C}$$ c'est impossible pour lui de deviner que le $= \widehat{AB'C}$ est obtenu à partir de $\widehat{ACB}$ et non $\widehat{C'AB}$ ! Ce conseil n'est pas valable que pour la géométrie : dans n'importe quel contexte, lorsqu'on écrit une égalité du type $W = X = Y = Z$, il faut que les égalités $W = X$, $X = Y$ et $Y = Z$ soient les égalités évidentes et que l'égalité $W = Z$ soit celle que l'on cherche à montrer.

  • Lorsqu'on donne des triangles semblables, il faut faire l'effort de lister les sommets de ces triangles dans le bon ordre. Ici il faut donc dire que $ABC'$ et $B'CA$ (et non $ACB'$) sont semblables. De cette manière, on peut directement vérifier l'égalité $\dfrac{|C'B|}{|AC|} = \dfrac{|AB|}{|B'C|}$ sans même se référer à la figure.

  • L'inégalité qui est écrite est presque illisible : il faut faire en sorte de la rendre plus lisible, par exemple en la centrant (avec des doubles dollars en $\LaTeX$). Idéalement on mettra chaque (in)égalité importante en évidence au centre pour faciliter la lecture.

  • Cela relève un peu plus de l'esthétique, mais l'étudiant utilise quatre fois "donc" dans cette solution de deux phrases. Il existe plein de façons de passer d'une affirmation à une autre, et on essayera en général d'utiliser différentes formulations pour rendre la solution moins rébarbative.

La solution suivante prend en compte toutes ces remarques, ce qui rend la solution bien plus facile et agréable à lire. Remarquez comme la solution est aérée. Même si elle parait plus longue que la solution précédente, elle est en fait beaucoup plus rapide à lire et à comprendre.

Solution 2 (bonne)
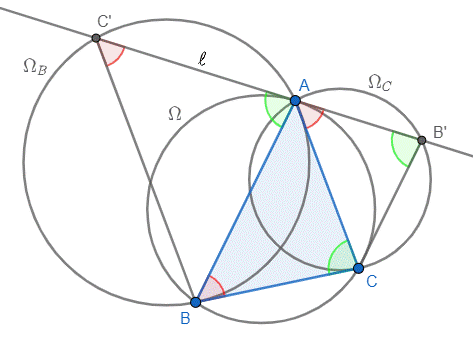
Notons $\Omega$ le cercle circonscrit à $ABC$, et $\Omega_B$ (respectivement $\Omega_C$) le cercle passant par $A$ et tangent à $BC$ en $B$ (respectivement $C$).

Par chasse aux angles, on trouve que $$\widehat{C'AB} = \widehat{ACB} = \widehat{AB'C},$$ par égalité d'angles tangentiel et inscrit dans $\Omega$ puis dans $\Omega_C$. De la même manière, on obtient que
$$\widehat{B'AC} = \widehat{ABC} = \widehat{AC'B}$$ par égalités d'angles tangentiel et inscrit dans $\Omega$ puis dans $\Omega_B$.

Les triangles $ABC'$ et $B'CA$ sont donc semblables, puisqu'ils ont deux paires d'angles en commun. En particulier, il vient que
$$\frac{|C'B|}{|AC|} = \frac{|AB|}{|B'C|}.$$ Par inégalité des moyennes arithmétique et géométrique, on déduit que
$$\frac 1 2 \cdot \left(\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|}\right) \ge \sqrt{\frac{|B'C|}{|AB|} \cdot \frac{|C'B|}{|AC|}} = 1,$$ ce qui implique bien que
$$\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2.$$